Data Structure

Linked List (II)

Circular Linked List 
Circular Linked List adalah Linked List di mana semua node terhubung untuk membentuk lingkaran. Tidak ada NULL di bagian akhir. Circular Linked List dapat berupa Circular Single Linked List atau Circular Doubly Linked List.

Circular Doubly Linked List 
Circular Doubly Linked List adalah jenis yang lebih kompleks dari Linked List yang berisi pointer ke node berikutnya serta sebelumnya dalam urutan. Sama seperti dengan Circular Single Linked List, tetapi total pointer pada setiap node adalah 2 pointer.

Doubly Linked List 
Doubly Linked List adalah elemen-elemen yang dihubungkan dengan dua pointer dalam satu elemen dan list dapat melintas baik di depan (head) atau belakang (tail).
Doubly Linked List berisi pointer tambahan, biasanya disebut pointer sebelumnya, bersama dengan pointer berikutnya dan data yang ada di Single Linked List.

Elemen-Elemen Dalam Doubly Linked List  
- Data
- Pointer Next ( *next )
- Pointer Prev ( *prev )

Doubly Linked List: Insertion
Sebuah node dapat ditambahkan dengan empat cara:
- Di bagian depan Doubly Linked List
- Setelah node yang diberikan
- Di bagian belakang Doubly Linked List
- Sebelum node yang diberikan
Contoh
Menambahkan node baru di belakang tail:

Doubly Linked List: Delete
4 hal yang harus diperhatikan saat melakukan delete:
- Node yang akan dihapus adalah satu-satunya node dalam Linked List.
- Node yang akan dihapus adalah head.
- Node yang akan dihapus adalah tail.
- Node yang akan dihapus bukan head atau tail.

Contoh
- Jika node yang akan di delete adalah satu-satunya node:

- Jika node yang akan di delete adalah head:

- Jika node yang akan di delete adalah tail:

- Jika node yang akan di delete bukan di head atau tail:

Doubly Linked List 

Doubly Linked List 

adalah elemen-elemen yang dihubungkan dengan dua pointer dalam satu elemen dan list dapat melintas baik di depan (head) atau belakang (tail).Doubly Linked List berisi pointer tambahan, biasanya disebut pointer sebelumnya, bersama dengan pointer berikutnya dan data yang ada di Single Linked List. 

Elemen-Elemen Dalam Doubly Linked List  
- Data
- Pointer Next ( *next )
- Pointer Prev ( *prev )

Doubly Linked List: Insertion
Sebuah node dapat ditambahkan dengan empat cara:
- Di bagian depan Doubly Linked List
- Setelah node yang diberikan
- Di bagian belakang Doubly Linked List
- Sebelum node yang diberikan

InsertionFront (push depan)
void insertFront(int num){
         struct data *curr = (struct data *)malloc(sizeof(struct data));
        curr->num = num;
        curr->next = NULL;
        if(head == NULL){
                    head = tail = curr;
                    head->prev = NULL;
        }else{
                 curr->next = head;
                 head->prev = curr;
                 head = curr;
        }
}

InsertionBack (push belakang)
void insert Back(int num){
         struct data *curr = (struct data *)malloc(sizeof(struct data));
        curr->num = num;
        curr->next = NULL;
        if(head == NULL){
                    head = tail = curr;
                    head->prev = NULL;
        }else{
                 tail->next = curr;
                 curr->prev =tail;
                 tail = curr;
        }
}

Doubly Linked List: Delete
4 hal yang harus diperhatikan saat melakukan delete:
- Node yang akan dihapus adalah satu-satunya node dalam Linked List.
- Node yang akan dihapus adalah head.
- Node yang akan dihapus adalah tail.
- Node yang akan dihapus bukan head atau tail

DeleteFront (pop depan)
void deleteFront(){
             struct data *curr = head;
             if(curr){
                       head = head->next;
                       free(curr);
                       head->prev = NULL;
             }
}

DeleteBack (pop belakang)
void deleteBack(){
             struct data *curr = head;
             if(curr){
                       tail = tail->prev;
                       free(curr);
                       tail->next = NULL;
             }
}


Hashing Tables & Binary Tree


Hashing
Hashing adalah teknik yang digunakan untuk menyimpan dan mengambil kunci dengan cepat.

Hashing digunakan untuk mengindeks dan mengambil item dalam database karena lebih cepat menemukan item menggunakan kunci hash yang lebih pendek daripada menemukannya menggunakan nilai asli.

Hash Table
Tabel hash adalah tabel (larik) tempat kami menyimpan string asli. Indeks tabel adalah kunci hash sementara nilainya adalah string asli.

Ukuran tabel hash biasanya beberapa urutan besarnya lebih rendah dari jumlah total string yang mungkin, sehingga beberapa string mungkin memiliki kunci hash yang sama.

Misalnya, ada 267 (8.031.810.176) string dengan panjang 7 karakter terdiri dari huruf kecil saja.

Operasi Pada Hash Tabel
-  insert: diberikan sebuah key dan nilai, insert nilai dalam tabel
-  find: diberikan sebuah key, temukan nilai yang berhubungan dengan key
-  remove: diberikan sebuah key,temukan nilai yang berhubungan dengan key 
-  getIterator: mengambalikan iterator,yang memeriksa nilai satu demi satu



Tree
Tree adalah struktur data non-linear yang mewakili hubungan hierarkis di antara objek data. Beberapa hubungan tree dapat diamati dalam struktur direktori atau hierarki organisasi. Node di tree tidak perlu disimpan secara berdekatan dan dapat disimpan di mana saja dan dihubungkan oleh pointer

Binary Tree
Binary tree adalah struktur data rooted tree di mana setiap node memiliki paling banyak dua anak. Kedua anak itu biasanya dibedakan sebagai anak kiri dan anak kanan. Node yang tidak memiliki anak disebut leaf.

Binary Search Tree

Binary Search Tree merupakan sebuah konsep penyimpanan data, dimana data disimpan dalam bentuk tree yang setiap node dapat memiliki anak maksimal 2 node. Selain itu, terdapat juga aturan dimana anak kiri dari parent selalu memiliki nilai lebih kecil dari nilai parent dan anak kanan selalu memiliki nilai lebih besar dari parent.

Binary Search Tree adalah struktur data pohon biner berbasis node yang memiliki properti berikut:

• Subtree kiri dari sebuah node hanya berisi node dengan kunci lebih rendah dari kunci node.
• Subtree kanan sebuah node hanya berisi node dengan kunci lebih besar dari kunci node.
• Subtree kiri dan kanan masing-masing juga harus berupa pohon pencarian biner.

Binary Search Tree memiliki 3 oprasi dasar, yaitu :

• Find(x)     : find value x didalam BST ( Search )
• Insert(x)   : memasukan value baru x ke BST ( Push )
• Remove(x)  : menghapus key x dari BST ( Delete )

Search BST

Bayangkan kita akan mencari value X.

• Memulai Pencarian Dari Root
• Jika Root adalah value yang kita cari , maka berhenti
• Jika x lebih kecil dari root maka cari kedalam rekrusif tree sebelah kiri
• Jika x lebih besar dari root maka cari kedalam rekrusif tree sebelah kanan

Insertion BST

Memasukan value (data) baru kedalam BST dengan rekrusif

Bayangkan kita menginsert value x :

• Dimulai dari root
• jika x lebih kecil dari node value(key) kemudian cek dengan sub-tree sebelah kiri lakukan pengecekan secara berulang ( rekrusif )
• jika x lebih besar dari node value(key) kemudian cek dengan sub-tree sebelah kanan lakukan pengecekan secara berulang ( rekrusif )
• Ulangi sampai menemukan node yang kosong untuk memasukan value X ( X akan selalu berada di paling bawah biasa di sebut Leaf atau daun )

Delete ( Remove )

akan ada 3 case yang ditemukan ketika ingin menghapus yang perlu diperhatikan :

• Jika value yang ingin dihapus adalah Leaf(Daun) atau paling bawah , langsung delete
• Jika value yang akan dihapus mempunyai satu anak, hapus nodenya dan gabungkan anaknya ke parent value yang dihapus
• jika value yang akan di hapus adalah node yang memiliki 2 anak , maka ada 2 cara , kita bisa cari dari left sub-tree anak kanan paling terakhir(leaf)

TREE

AVL Tree

AVL tree adalah Binary Search Tree (BST) yang dapat menyeimbangkan diri sendiri di mana perbedaan antara ketinggian subtree kiri dan kanan tidak boleh lebih dari satu untuk semua node.

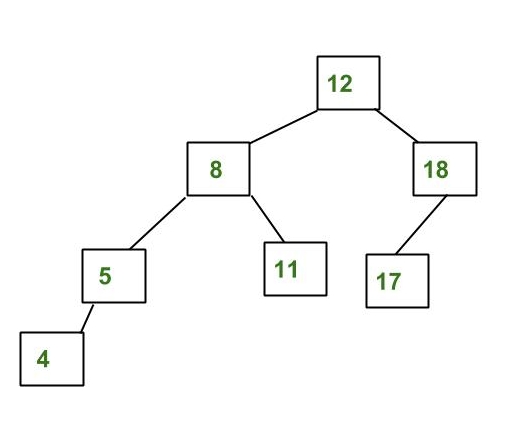
Pohon di atas adalah AVL karena perbedaan antara ketinggian sub pohon kiri dan kanan untuk setiap node kurang dari atau sama dengan 1.

Untuk memastikan bahwa pohon yang diberikan tetap AVL setelah setiap penyisipan, kita harus menambah operasi penyisipan BST standar untuk melakukan penyeimbangan ulang.

Waktu yang diperlukan untuk melakukan insertion, deletion, search, atau operasi lainnya bergantung pada ketinggian pohon, ini berarti mereka dapat menjadi O (n) dalam kondisi terburuk.

Balance factor:

Perbedaan ketinggian subtree KIRI dan subtree KANAN.

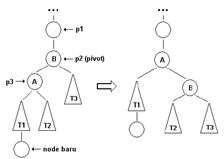
Single Rotation

Single rotation dilakukan bila kondisi AVL tree waktu akan ditambahkan node baru dan posisi node baru seperti pada gambar tersebut. T1, T2, dan T3 adalah subtree yang urutannya harus seperti demikian serta height- nya harus sama (≥ 0).

Double rotation dilakukan bila kondisi AVL tree waktu akan ditambahkan node baru dan posisi node baru seperti pada tersebut. T1, T2, T3, dan T4 adalah subtree yang urutannya harus seperti demikian. Tinggi subtree T1 harus sama dengan T4, tinggi subtree T2 harus sama dengan T3. Node yang ditambahkan akan menjadi child dari subtree T2 atau T3. 

HEAP and TRIES

Binary Heap

Binary Heap adalah Complete Binary Tree di mana item disimpan dalam urutan khusus sedemikian sehingga nilai dalam simpul parent lebih besar (atau lebih kecil) dari nilai-nilai dalam dua node child-nya. Yang pertama disebut sebagai max heap dan yang terakhir disebut min heap. Heap dapat diwakili oleh binary tree atau array.

1) Max Heap 
Selalu menyimpan nilai maksimum pada simpul root dan setiap simpul induk harus memiliki nilai simpul child yang lebih besar atau sama.

2) Min Heap 

Selalu menyimpan nilai minimum pada simpul root itu dan setiap simpul induk harus memiliki nilai yang lebih kecil atau sama dengan nilai simpul child itu.

Heap Sort Algorithm untuk mengurutkan dalam urutan yang meningkat:
1. Buat tumpukan maksimum dari data input.

2. Pada titik ini, item terbesar disimpan di root heap. Ganti dengan item terakhir heap diikuti dengan mengurangi ukuran heap oleh 1.

Contoh di atas menunjukkan dua skenario - satu di mana root adalah elemen terbesar dan kita tidak perlu melakukan apa pun. Dan yang lain di mana root memiliki elemen yang lebih besar sebagai seorang anak dan kami perlu bertukar untuk mempertahankan properti max-heap.

Terdapat sebuah skenario dimana ada lebih dari satu level:

Untuk mempertahankan properti max tree, terus mendorong 2 ke bawah hingga mencapai posisi yang benar.

TRIES

Trie adalah struktur data berupa pohon terurut untuk menyimpan suatu himpunan string dimana setiap node pada tree tersebut mengandung awalan (prefix) yang sama,
karena itulah trie disebut juga tree prefix. Trie sering digunakan pada masalah komputasi yang melibatkan penyimpanan dan pencarian string. Trie memiliki sejumlah keunggulan dibanding struktur data lain untuk memecahkan masalah serupa terutama dalam hal kecepatan dan memori yang digunakan. 

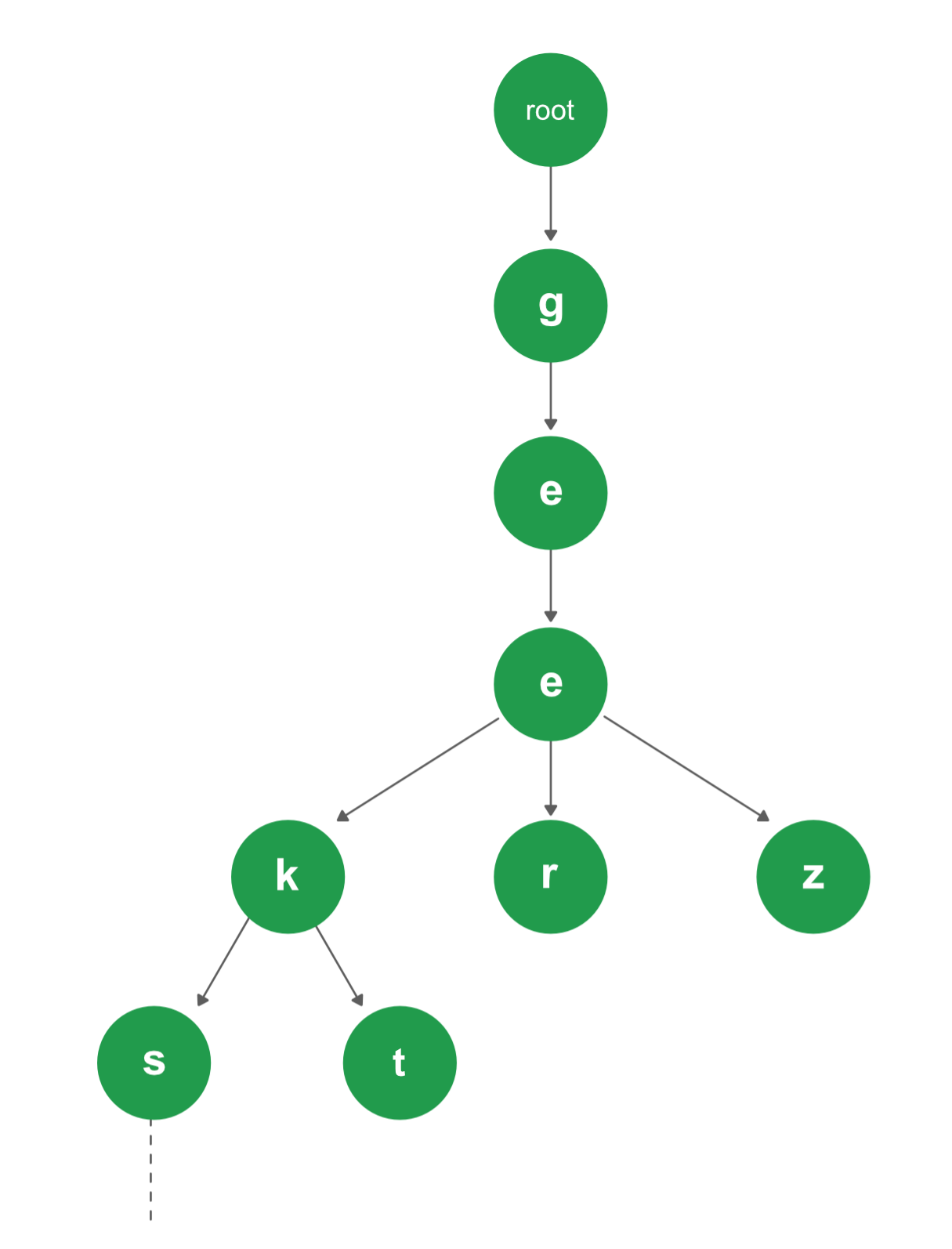
Setiap simpul Trie terdiri dari banyak cabang. Setiap cabang mewakili karakter kunci yang memungkinkan. Kita perlu menandai simpul terakhir dari setiap kunci sebagai simpul kata akhir.


Contoh Codingan Tries:

// Trie node
struct TrieNode
{
     struct TrieNode *children[ALPHABET_SIZE];

     // isEndOfWord is true if the node
     // represents end of a word
     bool isEndOfWord;
};

Dalam trie, tidak ada node yang menyimpan kunci yang terkait dengan node tersebut, sebaliknya, posisinya di pohon menunjukkan kunci apa yang terkait dengannya. Setiap keturunan dari sebuah node memiliki prefix yang sama dengan string yang diwakilkan oleh node tersebut, dan akar menandakan sebuah string kosong. 




Nama: Andre Christian Prasetyo
NIM: 2301850733